HARMONIQUE (ANALYSE)

HARMONIQUE (ANALYSE)

Lorsqu’on fait vibrer, dans des conditions idéales, une corde de longueur l , fixée en ses extrémités d’abscisses 0 et l , l’équation aux dérivées partielles:

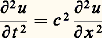est vérifiée, où u (x , t ) est une fonction dont la valeur représente, à l’instant t , le déplacement transversal, par rapport à la position d’équilibre, du point d’abscisse x .

D’Alembert donne, en 1747, la solution de cette équation sous la forme:

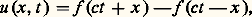où f est une fonction quelconque de période 2 l . Quelques années plus tard, en 1753, Daniel Bernoulli considère des solutions particulières de l’équation des cordes vibrantes, de la forme: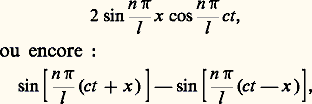

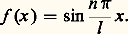pour toute valeur entière positive de n . Ces solutions correspondent aux fonctions f de la forme:

Or les fonctions trigonométriques:

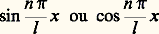sont les plus simples des fonctions de période 2 l . D’où l’idée, avancée par Bernoulli, que la fonction f la plus générale, qui intervient dans la solution de d’Alembert, peut s’exprimer sous la forme d’une série trigonométrique:

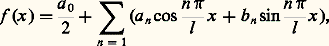ou, de manière équivalente:

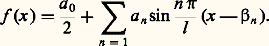Le terme correspondant à n = 1 donne alors la vibration fondamentale de la corde, les termes suivants correspondent aux harmoniques (cela rejoint l’expérience acoustique courante); de plus, le coefficient 見ⁿ régit l’intensité de l’harmonique d’ordre n , et 廓ⁿ en définit la phase.

Ainsi le problème des cordes vibrantes menait tout naturellement à la question suivante: une fonction périodique peut-elle se représenter par une série trigonométrique? L’analyse harmonique classique est, en principe, la branche des mathématiques qui traite de problèmes de ce type.

Pour obtenir des éléments de réponse à cette question fondamentale, il a fallu, à partir du milieu du XVIII^e siècle, que les mathématiciens se fassent une idée de plus en plus précise des objets sur lesquels ils travaillaient. C’est ainsi que l’étude de la représentation des fonctions périodiques par des séries trigonométriques devait fortement contribuer à la prise de conscience de la notion de fonction: la conception moderne d’une fonction, définie comme une correspondance, et pouvant fort bien ne posséder aucune des propriétés usuelles de régularité (continuité, dérivabilité, intégrabilité), émergea peu à peu lorsqu’il devint évident que l’idée naïve d’une fonction donnée par une formule explicite était insuffisante: il fallut tout à la fois préciser ce qu’on entendait par «fonction quelconque» et considérer des classes particulières de fonctions dont les propriétés spéciales, soigneusement mises en évidence, permettaient de résoudre un problème donné.

Ensuite, la théorie des distributions et celle des groupes topologiques sont venues proposer diverses directions dans lesquelles l’analyse harmonique se généralise et s’approfondit; celle-ci est devenue une branche importante des mathématiques, en relation avec les distributions, les algèbres normées, les probabilités, les espaces de Hilbert, les fonctions de variable complexe et s’est étendue aux fonctions non linéaires.

1. Les séries de Fourier

Les coefficients de Fourier

Considérons une fonction f à valeurs réelles ou complexes, d’une variable réelle, périodique, de période 2 神 pour fixer les idées. Si f admet un développement en série trigonométrique:

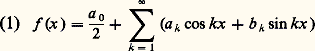et que la série (|a ^k | + |b ^k |) soit convergente, on peut intégrer terme à terme, entre 0 et 2 神, les séries: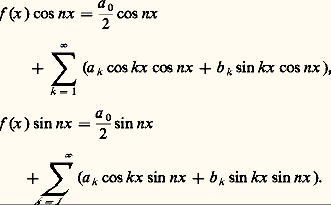

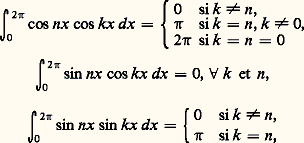Compte tenu des relations, valables pour des entiers n et k :

on obtient les valeurs des coefficients a ⁿ et b ⁿ directement à partir de la somme f (x ) de la série donnée:

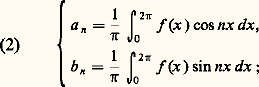ce sont les formules de Fourier.

Si, maintenant, on part d’une fonction f , de période 2 神, continue (il suffit, en fait, qu’elle soit intégrable, au sens de Lebesgue sur [0, 2 神]), il est naturel de considérer, par analogie avec ce qui précède, les coefficients a ⁿ et b ⁿ donnés, pour un entier n 閭 0, par les formules (2). Ce sont les coefficients de Fourier de la fonction f , et la série qu’ils définissent est la série de Fourier de f . Rien ne permet de préjuger de la convergence de cette série vers f , aussi la relation entre f et sa série de Fourier n’est-elle pas notée par le signe d’égalité, mais on écrit:

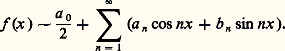Si, au lieu d’une fonction de période 2 神, on considère une fonction f de période T, on définit de manière analogue les coefficients de Fourier de f par les formules:

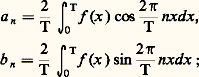la série de Fourier de f est alors:

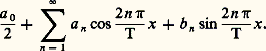Questions de convergence

Le problème de la représentation d’une fonction périodique par une série trigonométrique se ramène à l’étude de la convergence de sa série de Fourier. Nous nous contenterons de donner ici quelques-uns des nombreux résultats obtenus dans ce domaine ^{[cf. SÉRIES TRIGONOMÉTRIQUES]}.

a ) D’abord, en dehors de toute notion de convergence, la série de Fourier d’une fonction caractérise celle-ci (cela doit être compris comme une caractérisation en tant que fonction mesurable au sens de Lebesgue, deux fonctions étant considérées comme équivalentes lorsque l’ensemble des points où elles diffèrent est négligeable pour la mesure de Lebesgue: on dit alors qu’elles sont égales presque partout ^{[cf. INTÉGRATION ET MESURE]}; si l’on se restreint à la classe des fonctions continues, l’égalité presque partout entraîne l’égalité partout). Autrement dit, si deux fonctions ont les mêmes séries de Fourier, elles sont égales presque partout.

b ) Si les coefficients de Fourier, a ⁿ et b ⁿ , d’une fonction continue f forment une série absolument convergente (c’est-à-dire si la série (|a ⁿ | + |b ⁿ |) converge), alors la série de Fourier de f converge uniformément vers une fonction continue qui, d’après ce qui précède, a même série de Fourier que f . Le résultat ci-dessus montre donc que f est égale à la somme de sa série de Fourier.

Certains critères permettent d’affirmer qu’une fonction continue f possède la propriété ci-dessus. Montrons que c’est le cas si, par exemple, la fonction f admet une dérivée seconde continue. Soit a ⁿ et b ⁿ les coefficients de Fourier de f , a ⁿ et b ⁿ ceux de f , a ⁿ et b ⁿ ceux de f (f et f sont respectivement les dérivées première et seconde de f ). Une intégration par parties dans les intégrales (2) écrites pour f montre que l’on a:

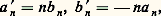et, par suite:

Or (2) entraîne que les coefficients de Fourier d’une fonction sont bornés en module (ils sont majorés par l’intégrale sur [0, 2 神] du module de cette fonction, divisée par 神), de sorte que la suite n ²(|a ⁿ | + |b ⁿ |) est bornée, ce qui montre que la série (|a ⁿ | + |b ⁿ |) converge. On obtient ainsi le résultat annoncé, qu’une fonction deux fois continûment dérivable est la somme de sa série de Fourier, la convergence étant d’ailleurs absolue et uniforme.

c ) Un résultat plus profond, dû à Dirichlet et à Jordan, est le suivant, que nous donnons dans un cas particulier: Si la fonction f , continue et périodique de période 2 神, possède une dérivée continue, sa série de Fourier converge uniformément vers f .

d ) Si l’on fait simplement l’hypothèse que f est continue, on ne peut plus affirmer que la série de Fourier de f converge vers f , ce qui signifierait que la suite des fonctions: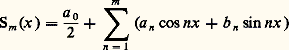

tend vers f lorsque m augmente indéfiniment. Au lieu des sommes partielles S^m de la série de Fourier de f , considérons les fonctions:

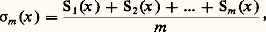appelées moyennes de Césaro de la fonction f . On a alors le théorème de Fejer: Si f est continue, ses moyennes de Césaro tendent uniformément vers f .

Coefficients de Fourier exponentiels

Si l’on introduit la fonction exponentielle complexe e ^ix , liée aux fonctions trigonométriques par les relations d’Euler:

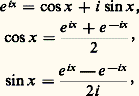on obtient l’égalité: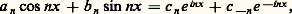

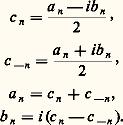où les coefficients a ⁿ , b ⁿ , c ⁿ , c ^-n vérifient les relations:

Si f est périodique et intégrable, on appellera coefficients de Fourier exponentiels les nombres c ⁿ , définis pour tout entier relatif n , par:

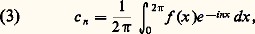et on appellera encore série de Fourier de f ^{[cf. SÉRIES TRIGONOMÉTRIQUES]} la série:

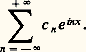Moyennant les relations ci-dessus entre les a ⁿ , b ⁿ (n 閭 0) et c ⁿ (n quelconque), il y a identité formelle entre cette notion de série de Fourier et la notion antérieure de série de Fourier trigonométrique (où l’on peut introduire un coefficient b ⁰ égal à 0).

Nous utiliserons désormais la forme «exponentielle» de la série de Fourier d’une fonction f :

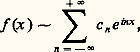qui donne des calculs et des formules plus simples, et correspond mieux à la nature profonde de la situation mathématique, comme nous le verrons au chapitre 4.

Le théorème de Bessel-Parseval-Plancherel

Soit f une fonction périodique continue, et soit:

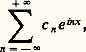sa série de Fourier. On a alors l’égalité suivante:

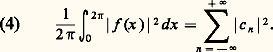Plus généralement, si on considère une fonction périodique, de carré intégrable sur [0, 2 神], cette fonction est en particulier intégrable, et possède des coefficients de Fourier c ⁿ tels que l’égalité (4) ait lieu.

Tout aussi remarquable est le fait que toute suite (c ⁿ ), n parcourant l’ensemble des entiers relatifs, telle que:

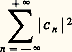converge, est la suite des coefficients de Fourier d’une fonction de carré intégrable.

En d’autres termes, la correspondance entre une fonction de carré intégrable sur [0, 2 神] et la suite de ses coefficients de Fourier définit un isomorphisme isométrique entre l’espace de Hilbert L²([0, 2 神]) et l’espace de Hilbert l ² des suites de carré intégrable (les structures hilbertiennes des deux espaces ci-dessus sont définies par les produits scalaires:

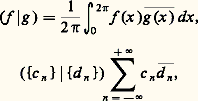la convergence de l’intégrale et de la série étant assurée par l’inégalité de Schwarz; cf. INTÉGRATION ET MESURE, espace de HILBERT, D. HILBERT).

Pour les fonctions périodiques de carré intégrable sur [0, 2 神], les méthodes hilbertiennes simplifient l’étude des séries de Fourier. Citons par exemple le résultat suivant, dont la démonstration est d’ailleurs facile: Si f est périodique, de carré intégrable sur [0, 2 神], la série de Fourier: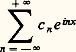

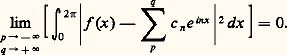de f converge vers f au sens de l’espace L²; cela signifie que:

Les fonctions presque-périodiques

La somme de deux fonctions périodiques dont les périodes sont dans un rapport irrationnel n’est pas périodique (par exemple, e ^ix +e size=1^漣i size=1^神x , sin x +cos 連2x sont des modèles de telles fonctions). Cependant, les fonctions de ce type ont des propriétés voisines de la périodicité. Cette idée a conduit Harald Bohr, vers 1925, à la notion de fonction presque-périodique.

Une fonction f , continue sur la droite réelle, est appelée presque-périodique si, pour tout 﨎 礪 0, il existe un nombre T 礪 0 tel que tout intervalle de longueur T contienne au moins un nombre c tel que l’on ait:

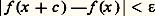pour toute valeur réelle de la variable x . Une fonction périodique possède évidemment cette propriété. De nombreuses définitions équivalentes de la presque-périodicité peuvent être données; en voici une: Une fonction est presque-périodique si, et seulement si, elle peut être approchée uniformément par une suite de fonctions de la forme:

où les c ⁿ sont des nombres complexes et lesⁿ des nombres réels.

Les fonctions presque-périodiques forment un anneau, et toute limite uniforme d’une suite de fonctions presque-périodiques est une fonction presque-périodique.

Pour toute fonction presque-périodique f , l’expression: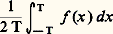

possède une limite lorsque T tend vers l’infini. Cette limite, notée M(f ), est appelée valeur moyenne de f .

Par le biais des moyennes, on peut définir la série de Fourier d’une fonction presque-périodique. Pour tout réel, la fonction f (x )e size=1^漣i size=1^凞x est presque-périodique; appelons c size=1^凞 sa moyenne. On montre que les valeurs de telles que c size=1^凞 ne soit pas nul forment un ensemble fini ou dénombrable¹,², ...,ⁿ , ...; on appelle série de Fourier de f l’expression:

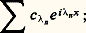lorsque f est périodique de période 2 神, lesⁿ sont entiers et on retrouve la notion usuelle de série de Fourier.

Les séries de Fourier des fonctions presque-périodiques jouissent de propriétés analogues à celles des séries de Fourier des fonctions périodiques. Citons par exemple le résultat suivant, analogue à la relation (4): Pour toute fonction presque-périodique f , |f |² est presque-périodique et, si c ⁿ e ⁱ size=1^{凞n x} est la série de Fourier de f , on a:

2. Analyse et synthèse harmoniques

Considérons une fonction f continue, de période 2 神, et soit: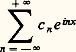

sa série de Fourier. L’égalité:

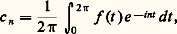entraîne: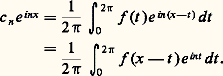

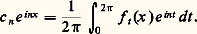Si nous appelons f ^t la translatée de f par t , définie par f ^t (x ) = f (x 漣 t ), nous obtenons:

En considérant l’intégrale comme une limite de sommes finies, on peut dire, de manière peu précise mais imagée, que c ⁿ e ^inx (ou aussi bien e ^inx lorsque c ⁿ n’est pas nul) est limite de combinaisons linéaires de translatées de f .

Cela nous conduit à la notion d’analyse harmonique et de spectre d’une fonction. Soit E un espace vectoriel topologique (cf. espaces vectoriels TOPOLOGIQUES) de fonctions définies sur l’ensemble R des nombres réels, tel que si f 捻 E et t 捻 R, la translatée f ^t appartienne à E, avec certaines conditions de continuité; on suppose, de plus, que toute fonction exponentielle e ⁱ size=1^凞x , réel, appartient à E.

On dira qu’un nombre réel appartient au spectre d’un élément f de E si la fonction e ⁱ size=1^凞x peut être approchée, au sens de la topologie de E, par des combinaisons linéaires de translatées de f . On note 靖^E(f ), spectre de f dans E, l’ensemble des tels (pour une fonction donnée, la notion de spectre peut dépendre de la topologie dont est muni l’espace E).

Le problème de l’analyse harmonique dans E d’une fonction f est la détermination de 靖^E(f ). Le problème de la synthèse harmonique dans E de f est le suivant: f est-elle limite, dans E, de combinaisons linéaires d’exponentielles, e ⁱ size=1^凞x , avec 捻 靖^E(f )? Si la réponse est positive, on dit que f satisfait à la synthèse harmonique (ou encore que f est synthétisable) dans E.

Prenons, par exemple, pour E l’espace des fonctions continues et bornées sur R, avec la topologie de la convergence uniforme. Si f est une fonction périodique appartenant à E, le spectre de f est l’ensemble des entiers n tels que les coefficients de Fourier c ⁿ correspondants soient non nuls; le théorème de Fejer sur la convergence uniforme vers f des moyennes de Césaro montre que f est synthétisable dans E. Plus généralement, si f est presque-périodique, de série de Fourier:

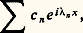avec c ⁿ 0, le spectre de f est l’ensemble des exposantsⁿ qui figurent dans la série de Fourier de f . Pour une fonction continue et bornée quelconque, le spectre est plus difficile à déterminer en général. Il est remarquable que, dans l’espace E que nous considérons ici, les fonctions synthétisables soient exactement les fonctions presque-périodiques.

En fait, les questions les plus intéressantes concernant la synthèse harmonique se posent lorsque l’on prend pour E l’espace L size=1^秊(R), muni de sa topologie faible d’espace dual de L¹(R) (cf. INTÉGRATION ET MESURE, et espaces vectoriels TOPOLOGIQUES). Ces problèmes, ainsi que leur généralisation au cas où l’on considère d’autres groupes que R (cf. chap. 4) sont loin d’être tous résolus et leur étude est l’un des points essentiels de l’analyse harmonique moderne.

3. La transformation de Fourier

Certaines classes importantes de fonctions ne se prêtent pas à l’analyse harmonique telle qu’elle a été définie ci-dessus. Ainsi, l’espace L¹(R) des (classes de) fonctions intégrables sur R ne contient aucune exponentielle; aussi utilise-t-on un autre procédé pour en faire l’analyse et la synthèse. C’est la transformation de Fourier qui permet de définir le spectre d’une fonction intégrable et, dans certains cas, d’en faire la synthèse.

Soit f une fonction intégrable (par exemple, continue et nulle hors d’un ensemble borné). À f on associe une autre fonction définie sur R, notée f ou 杻f , et appelée transformée de Fourier de f :

La présence du coefficient 漣 2 神 est conventionnelle (la convention n’est d’ailleurs pas universelle) et permet d’avoir une formule de réciprocité particulièrement simple.

Définissons, outre l’opérateur 杻 de transformation de Fourier, l’opérateur 杻 漣 de transformation de Fourier conjuguée (ou réciproque):

Pour toute fonction f , et tout réel t , on a:

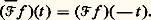Propriétés de la transformation de Fourier

a ) Pour toute fonction intégrable f , 杻f est continue et tend vers 0 à l’infini. Si on désigne par A(R) l’ensemble des fonctions 杻f , pour f 捻 L¹(R), A(R) est donc un sous-espace de l’espace vectoriel C⁰(R) des fonctions continues sur R qui tendent vers 0 à l’infini. En fait, A(R) est strictement plus petit que C⁰(R).

b ) Si f et g sont intégrables, leur produit de convolution f g , défini par:

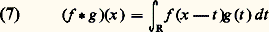l’est également. On a alors la relation:

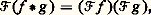de sorte que A(R) est un anneau de fonctions continues sur R, de même que L¹(R) est un anneau pour la convolution. Cette circonstance permet d’appliquer à l’étude de A(R) et de L¹(R) la théorie des algèbres normées (cf. algèbres NORMÉES), qui en est d’ailleurs issue en grande partie.

c ) Si y et u sont des réels, 﨏 une fonction, on définit les fonctions 﨏^y , 﨏^u , 﨏 漣, 﨏, 﨏 par:

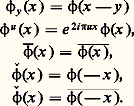On a alors:

d ) Si f est dérivable et si f et f sont intégrables, on a:

e ) Si f est intégrable, ainsi que son produit par x , alors 杻f est dérivable et on a:

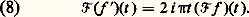
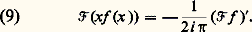Il est intéressant de voir comment certaines propriétés des fonctions se traduisent sur leurs transformées de Fourier.

Par exemple, les relations (8) et (9) montrent que plus une fonction est régulière (dérivable), plus sa transformée de Fourier tend rapidement vers 0 à l’infini. Inversement, plus f tend rapidement vers 0 à l’infini, plus 杻f est régulière. Voici un autre exemple, présenté en termes vagues: plus les valeurs d’une fonction sont concentrées autour de l’origine, plus celles de sa transformée de Fourier sont, au contraire, étalées.

Le théorème de réciprocité

De même que la série de Fourier d’une fonction périodique caractérise celle-ci, sans qu’aucune propriété de convergence soit nécessaire, la transformée de Fourier d’une fonction f caractérise cette fonction. Donc la donnée de 杻f contient toute l’information relative à f . Dans certains cas, il est possible d’exprimer f explicitement à partir de 杻f .

Théorème. Si f et 杻f sont toutes deux intégrables, on a:

C’est là une remarquable propriété de symétrie entre les opérateurs 杻 et 杻 漣.

On peut encore interpréter cela comme une propriété de synthèse: si on appelle spectre de f le support de sa transformée de Fourier 杻f , c’est-à-dire l’adhérence de l’ensemble des points où 杻f ne s’annule pas, le théorème de réciprocité, lorsque 杻f est intégrable, s’écrit: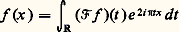

et exprime que f est, en un certain sens, synthétisable, puisque f (x ) s’exprime sous la forme d’une intégrale (donc comme limite de combinaisons linéaires) à partir des exponentielles qui correspondent à des valeurs t contenues dans son spectre.

Une classe très importante de fonctions se prête à l’utilisation du théorème de réciprocité: c’est la classe 崙 des fonctions indéfiniment dérivables à décroissance rapide. Une fonction f appartient à 崙 si, et seulement si, elle admet des dérivées de tous les ordres et si, quels que soient les entiers n et p :

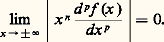Les relations (8) et (9) montrent que si f appartient à 崙, il en est de même pour 杻f , et réciproquement. De sorte que 杻 est un isomorphisme linéaire de 崙 sur 崙, dont 杻 漣 est l’isomorphisme réciproque. En fait, si on considère la topologie usuelle de 崙 (cf. DIS- TRIBUTIONS), face=F0021 杻 et 杻 漣 sont des isomorphismes continus.

Extension aux distributions tempérées

Rappelons brièvement (cf. DISTRIBUTIONS) que, si l’on désigne par 崙 l’espace des distributions tempérées, espace dual de 崙, la transformation de Fourier sur 崙 permet de définir, par transposition, la notion de transformation de Fourier sur 崙 qui fournit un isomorphisme de 崙 sur 崙 . Cela donne d’intéressantes applications, par exemple, à l’étude d’équations différentielles, ou plus généralement d’équations de convolution (lorsque l’on étend cette théorie aux espaces Rⁿ de dimension supérieure à 1, on peut traiter par ce procédé des équations aux dérivées partielles linéaires à coefficients constants). D’après la propriété b , une telle équation est transformée par Fourier en une équation qui pourra, dans certains cas, se résoudre par division. Par exemple, un opérateur différentiel linéaire à coefficients constants (convolution par une combinaison linéaire de dérivées de la mesure de Dirac en 0) devient, par transformation de Fourier, l’opérateur de multiplication par un polynôme.

Ces idées sont à rapprocher de la transformation de Laplace ^{[cf. SYMBOLIQUE]}.

Transformation de Fourier-Plancherel dans L² (R)

Les espaces L¹(R) et L²(R) ne sont pas inclus l’un dans l’autre. Mais ils contiennent tous deux l’ensemble K(R) des fonctions continues nulles hors d’un ensemble borné, et tout élément de L¹(R) ou de L²(R) peut être approché, au sens de L¹ ou de L² selon le cas, par des éléments de K(R).

Si f appartient à K(R), face=F0021 杻f appartient à L²(R), et on a l’égalité:

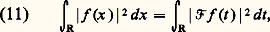formellement analogue à (4).

Cette relation permet d’étendre à L²(R) la transformation de Fourier (aussi bien que la transformation de Fourier réciproque): on obtient ainsi un opérateur, toujours noté 杻, de L²(R) dans L²(R) qui coïncide avec la notion précédente de transformation pour les fonctions qui, comme celles de K(R), appartiennent à la fois à L¹(R) et à L²(R).

Pour f dans L²(R), on écrit aussi parfois:

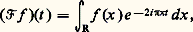bien que cette formule n’ait pas de sens pour deux raisons: d’abord, l’intégrale peut ne pas être convergente; ensuite 杻f est un élément de L²(R), donc défini à un ensemble de mesure nulle près, et on ne peut pas considérer la valeur d’un tel objet en un point particulier.

Ce nouvel opérateur de L²(R) dans L²(R), appelé transformation de Fourier-Plancherel, est un isomorphisme isométrique de L²(R), dont l’isomorphisme réciproque est 杻 漣 (plus exactement, l’extension de 杻 漣 à L²).

Pour f et g dans L²(R), on a l’identité de Parseval, qui exprime précisément l’isomorphisme de l’espace de Hilbert L²(R) dans lui-même défini par 杻:

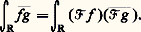Cela permet, comme pour les séries trigonométriques, d’exploiter, dans l’analyse harmonique des fonctions de carré intégrable, la puissance de la théorie des espaces de Hilbert.

Généralisations

La transformation de Fourier que nous avons introduite pour les fonctions d’une variable réelle se généralise sans peine aux fonctions de plusieurs variables réelles.

Soit f une fonction intégrable sur Rⁿ (n entier 閭 1). On définit la transformée de Fourier de f comme la fonction de n variables définie sur Rⁿ par:

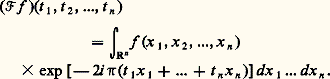Les propriétés sont, en dimension n , tout à fait analogues à celles que l’on a en dimension 1.

Une autre direction de généralisation consiste à définir la transformée de Fourier de f non seulement pour des valeurs réelles de t , mais aussi pour certaines valeurs complexes. On pose:

fonction définie pour certaines valeurs de z . Lorsque f est, par exemple, nulle pour les valeurs négatives de x , on retrouve la notion de transformée de Laplace ^{[cf. SYMBOLIQUE]}.

Lorsque 杻f (z ) peut être définie pour toute valeur de z , on peut déduire du comportement de la fonction de variable complexe obtenue de nombreux renseignements sur la fonction f donnée (théorème de Paley-Wiener, par exemple).

4. Les groupes commutatifs localement compacts

La mesure de Haar

La démonstration par Haar, en 1933, de l’existence d’une mesure invariante par translation, sur une large classe de groupes topologiques, permet, à partir de cette époque, de situer l’analyse harmonique dans sa vraie perspective et d’en comprendre la nature profonde.

Si on considère, sur R, la mesure de Lebesgue dx , on constate qu’elle est invariante par translation, en ce sens que, pour toute fonction intégrable f et tout réel t , la translatée f ^t est intégrable et a même intégrale que f . De même, sur le groupe multiplicatif des nombres complexes de module 1, que l’on peut, en ce qui concerne la théorie de la mesure, identifier à l’intervalle [0, 2 神], la mesure de Lebesgue est invariante par translation, car, pour toute fonction intégrable f , et tout de module 1, on a: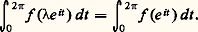

Parmi les groupes topologiques, ceux qui sont localement compacts (cette classe contient, entre autres, les groupes de Lie) possèdent une propriété analogue.

Pour une fonction f définie sur un groupe G, et un élément t du groupe, on considère les translatées ^t f et f ^t de f par t , respectivement à gauche et à droite, données par:

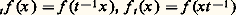(le groupe est noté multiplicativement). Il y a lieu de distinguer les translations à gauche et à droite si G n’est pas commutatif. Lorsque G possède la propriété de compacité locale, le théorème de Haar affirme l’existence (et l’unicité à un facteur multiplicatif près) d’une mesure ^{[cf. INTÉGRATION ET MESURE]} invariante par les translations à gauche, c’est-à-dire telle que, pour tout t 捻 G et toute fonction intégrable f , ^t f soit intégrable et de même intégrale que f . Il y a également une mesure invariante par les translations à droite, mais elle diffère en général de la mesure invariante à gauche (pour les groupes compacts, ces deux types de mesures sont identiques, de même que pour les groupes commutatifs). Une telle mesure est appelée mesure de Haar à gauche (ou à droite, selon le cas). Si 猪 est une mesure de Haar à gauche, f une fonction 猪-intégrable et t un élément de G, on a donc:

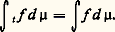Le théorème de Haar et l’étude des représentations linéaires des groupes topologiques forment le cadre de l’analyse harmonique abstraite.

Nous allons donner un bref aperçu de cette théorie dans le cadre des groupes commutatifs localement compacts, où elle est beaucoup plus simple et plus développée.

Le théorème de dualité de Pontriaguine et Van Kampen

Soit G un groupe commutatif localement compact; l’opération de G est notée additivement, 0 désigne l’élément neutre.

On appelle caractère de G tout homomorphisme continu de G dans le groupe multiplicatif des nombres complexes de module 1. Autrement dit, un caractère est une fonction continue 塚 sur G, telle que, quels que soient x et y dans G:

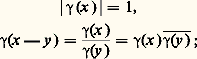on en déduit, évidemment:

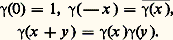Si 塚 et 塚 sont deux caractères, la fonction qui, à tout x de G, associe 塚(x ) 塚 (x ) est encore un caractère que l’on note 塚 + 塚 . Il est facile de voir que l’on peut ainsi munir l’ensemble des caractères sur G d’une structure de groupe commutatif, que l’on rend localement compact en y considérant une topologie particulière (c’est la topologie de la convergence uniforme sur les parties compactes de G).

Notons G le groupe commutatif localement compact formé des caractères de G. Ce groupe est appelé dual de G. On peut considérer le dual de G, qui est un groupe commutatif localement compact G.

Pour tout x de G, la fonction définie sur G par 塚塚(x ) est un caractère sur G, donc un élément de G. On a ainsi une application de G dans G.

Le résultat fondamental établi, vers 1935, par Pontriaguine et Van Kampen est le suivant: L’application de G dans G définie ci-dessus est un isomorphisme topologique. En d’autres termes, le dual du dual d’un groupe G s’identifie à G lui-même.

Eu égard à la dualité, on notera indifféremment:

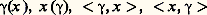le nombre complexe égal à la valeur en x 捻 G du caractère 塚 sur G, ou à la valeur en 塚 捻 G du caractère x sur G.

Soit par exemple, Z le groupe additif des entiers relatifs. Un caractère 塚 sur Z est déterminé par la valeur 塚(1) = 見, car 塚(n ) = 見ⁿ pour tout n 捻 Z. Réciproquement, tout nombre 見 de module 1 définit un caractère 塚 sur Z (tel que 塚(1) = 見), par la formule 塚(n ) = 見ⁿ . On identifie ainsi le dual de Z au groupe multiplicatif T des nombres complexes de module 1. D’après le théorème de dualité, les caractères sur T correspondent aux nombres entiers: tout caractère sur T est de forme 見見ⁿ pour un entier n ; cela peut d’ailleurs se voir directement. Pour le groupe R des nombres réels, un caractère est une fonction continue 﨏 telle que:

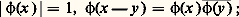une telle fonction est nécessairement de la forme xe ²ⁱ size=1^神tx , où t est un paramètre réel; à la somme t + t correspond le produit des caractères définis par t et t ; ainsi le groupe dual de R s’identifie à R lui-même.

La transformation de Fourier

Soit G un groupe commutatif localement compact, G le groupe dual de G, dx une mesure de Haar sur G.

À toute fonction intégrable f sur G, on associe une fonction f sur G, la transformée de Fourier de f , définie, pour tout 塚 捻 G, par:

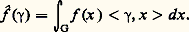Si G = T, G = Z et la fonction f est alors une suite, qui n’est autre que la suite des coefficients de Fourier de f (on peut considérer f indifféremment comme une fonction sur T, ou comme une fonction sur R de période 2 神: on identifie les points de R congrus à t modulo 2 神 au nombre complexe e^it de module 1); si G = R, G = R et f est la transformée de Fourier usuelle (sur R) de f . Ainsi l’étude des séries et intégrales de Fourier apparaît comme un cas particulier de la transformation de Fourier abstraite.

La transformation de Fourier abstraite jouit de propriétés semblables à celles que nous avons vues dans le cas des fonctions de variable réelle. Citons-en quelques-unes.

a ) Si f est intégrable sur G, f est continue sur G.

b ) f 令 0 si, et seulement si, f 令 0. Autrement dit, f caractérise parfaitement f .

c ) Soit f et g deux fonctions intégrables sur G. Alors la fonction f g , définie sur G par:

est intégrable, et: (f g ) = f g .

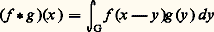Ainsi, l’ensemble A(G) des transformées de Fourier des fonctions intégrables sur G est une algèbre. Les méthodes générales de la théorie des algèbres normées s’appliquent à l’étude de nombreuses propriétés de A(G), ou aussi bien de l’algèbre de convolution L¹(G).

d ) Formule de réciprocité. On peut choisir les mesures de Haar dx et d 塚 de G et de G (qui dépendent d’un facteur constant que l’on peut ajuster) de telle sorte que, lorsque f est intégrable sur G, et f intégrable sur G, l’on ait, pour tout x 捻 G et tout 塚 捻 G:

e ) Théorème de Bessel-Parseval-Plancherel : Si f est à la fois intégrable et de carré intégrable sur G, f est de carré intégrable sur G et on a, avec le même choix des mesures de Haar que ci-dessus: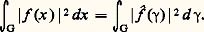

Cela permet, comme dans le cas réel, de définir une transformation de Fourier-Plancherel qui est un isomorphisme isométrique de L²(G) sur L²(G). Ici encore, les méthodes propres aux espaces de Hilbert s’appliquent avec fruit.

Ainsi, l’étude des groupes commutatifs localement compacts offre à l’analyse harmonique son cadre naturel, et l’étude abstraite permet de retrouver et d’approfondir la théorie de l’analyse harmonique sur R et celle des séries de Fourier. Bien entendu, des propriétés liées à la structure particulière de R (comme celles qui se rattachent à la dérivation, l’extension aux distributions, par exemple) ne sont pas susceptibles d’un tel traitement abstrait. Aussi l’analyse harmonique continue-t-elle à se développer sur les deux plans, dans le cadre abstrait des groupes commutatifs localement compacts, et dans le cadre classique de la droite réelle et des espaces Rⁿ .

Notons enfin que, si l’on considère des groupes localement compacts non commutatifs, il existe – surtout dans le cadre des groupes de Lie – une théorie similaire, mais beaucoup plus éloignée de la situation «classique» de l’analyse harmonique sur R (par exemple l’objet dual n’est plus un groupe, la transformée de Fourier d’une fonction n’est plus une fonction numérique, etc.), et qui fait actuellement l’objet d’un développement rapide.

Encyclopédie Universelle. 2012.